El primer estudio formal sobre el tema fue realizado por el matemático
y más tarde reformulada por Zermelo.
El concepto de conjunto es intuitivo y se podría definir como una "agrupación bien definida
de objetos no repetidos y no ordenados"; así, se puede hablar de un conjunto de personas,
ciudades, gafas, lapiceros o del conjunto de objetos que hay en un momento dado encima
de una mesa. Un conjunto está bien definido si se sabe si un determinado elemento pertenece
o no al conjunto. El conjunto de los bolígrafos azules está bien definido, porque a la vista de
un bolígrafo se puede saber si es azul o no. El conjunto de las personas altas no está bien
definido, porque a la vista de una persona, no siempre se podrá decir si es alta o no, o puede
haber distintas personas, que opinen si esa persona es alta o no lo es. En el siglo XIX, según
Frege, los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la
teoría de conjuntos está bien definida por el sistema ZFC. Sin embargo, sigue siendo célebre
la definición que publicó Cantor.
Se entiende por conjunto a la agrupación en un todo de objetos bien diferenciados de nuestra
intuición o nuestro pensamiento.
A propósito de la noción de conjunto, Dedekind dijo que se los imaginaba como un saco cerrado
que contiene cosas... de las que no sabemos nada fuera de que existen y son totalmente determinadas.
Algún tiempo después, Cantor dio a conocer su idea de conjunto: elevó su colosal figura, describió
con el brazo erguido un gesto soberbio, y dijo con la mirada perdida:
'Me imagino un conjunto como
un abismo'.
Usualmente los conjuntos se representan con una letra mayúscula: A, B, K,...
Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto,
estos elementos tienen carácter individual, tienen cualidades que nos permiten
diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o
repetidos. Los representaremos con una letra minúscula: a, b, k,...
De esta manera, si  es un conjunto, y
es un conjunto, y  todos sus elementos, es común escribir:
todos sus elementos, es común escribir:
 es un conjunto, y
es un conjunto, y  todos sus elementos, es común escribir:
todos sus elementos, es común escribir:para definir a tal conjunto  . Esta notación empleada para definir al conjunto
. Esta notación empleada para definir al conjunto 
 . Esta notación empleada para definir al conjunto
. Esta notación empleada para definir al conjunto 
se llama notación por extensión.
Para representar que un elemento  pertenece a un conjunto A, escribimos
pertenece a un conjunto A, escribimos 
 pertenece a un conjunto A, escribimos
pertenece a un conjunto A, escribimos 
(léase "x en A", "x pertenece a A" o bien "x es un elemento de A"). La negación
de  se escribe
se escribe 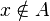 (léase
(léase  no pertenece a
no pertenece a  ).
).
 se escribe
se escribe 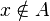 (léase
(léase  no pertenece a
no pertenece a  ).
).El conjunto universal, que siempre representaremos con la letra U (u mayúscula),
es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos
de números enteros entonces U es el conjunto de los números enteros, si hablamos
de ciudades, U es el conjunto de todas las ciudades, este conjunto universal puede
mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el
contexto que estemos tratando, pero siempre es necesario demostrar la existencia de
dicho conjunto previamente.
Existe además, un único conjunto que no tiene elementos al que se le
llama conjunto vacío y que se denota por  . Es decir
. Es decir
 . Es decir
. Es decirLa característica importante de este conjunto es que satisface todos los elementos posibles
que no están contenidos en él, es decir
 .
.
Por otro lado, si todos los elementos  de un conjunto A satisfacen alguna propiedad,
de un conjunto A satisfacen alguna propiedad,
 de un conjunto A satisfacen alguna propiedad,
de un conjunto A satisfacen alguna propiedad, misma que pueda ser expresada como una proposición  , con la indeterminada
, con la indeterminada  , usamos l
, usamos l
 , con la indeterminada
, con la indeterminada  , usamos l
, usamos la notación por comprensión, y se puede definir:
Lo anterior se lee "A es el conjunto de elementos x, que cumplen la propiedad p(x)".
El símbolo ":" se lee "que cumplen la propiedad" o "tal que"; este símbolo puede ser
remplazado por una barra  .
.
 .
.Por ejemplo, el conjunto  puede definirse por:
puede definirse por:
 puede definirse por:
puede definirse por:donde el símbolo  representa al conjunto de los números naturales.
representa al conjunto de los números naturales.
 representa al conjunto de los números naturales.
representa al conjunto de los números naturales.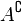

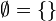


No hay comentarios:
Publicar un comentario