Al describir grupos de observaciones, con frecuencia es conveniente resumir la información con un solo número. Este número que, para tal fin, suele situarse hacia el centro de la distribución de datos se denomina medida o parámetro de tendencia central o de centralización. Cuando se hace referencia únicamente a la posición de estos parámetros dentro de la distribución, independientemente de que ésta esté más o menos centrada, se habla de estas medidas comomedidas de posición.1 En este caso se incluyen también los cuantiles entre estas medidas.
Entre las medidas de tendencia central tenemos:
Media Aritmética
En matemáticas y estadística, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales
Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.
Definición
Dados los n números 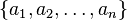 , la media aritmética se define simplemente como:
, la media aritmética se define simplemente como:
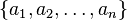 , la media aritmética se define simplemente como:
, la media aritmética se define simplemente como:Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:
Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra (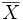 ), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
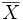 ), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.
), mientras que la letra µ (mi) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.Mediana (Estadística)
En el ámbito de la estadística, una mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. La mediana coincide con el percentil 50, con el segundo cuartil y con el quinto decil.
Existen dos estrategias para calcular la mediana: considerando los datos en forma individual, sin agruparlos, o bien utilizando los datos agrupados en intervalos de clase. Veamos cada una de ellas.
[editar]Datos sin agrupar
Sean 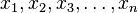 los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:
los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:
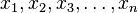 los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:
los datos de una muestra ordenada en orden creciente y designando la mediana como Me, distinguimos dos casos:a) Si n es impar, la mediana es el valor que ocupa la posición (n + 1) / 2 una vez que los datos han sido ordenados (en orden creciente o decreciente), porque éste es el valor central. Es decir: Me = x(n + 1) / 2.
Por ejemplo, si tenemos 5 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9 => El valor central es el tercero: x(5 + 1) / 2 = x3 = 7. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (x1, x2) y otros dos por encima de él (x4, x5).
b) Si n es par, la mediana es la media aritmética de las dos observaciones centrales. Cuando n es par, los dos datos que están en el centro de la muestra ocupan las posiciones n / 2 y n / 2 + 1. Es decir: Me = (xn / 2 + xn / 2 + 1) / 2.
Por ejemplo, si tenemos 6 datos, que ordenados son: x1 = 3, x2 = 6, x3 = 7, x4 = 8, x5 = 9, x6 = 10 => Hay dos valores que están por debajo del 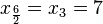 y otros dos que quedan por encima del siguiente dato
y otros dos que quedan por encima del siguiente dato  . Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos:
. Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos: 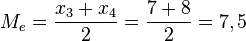 .
.
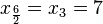 y otros dos que quedan por encima del siguiente dato
y otros dos que quedan por encima del siguiente dato  . Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos:
. Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos: 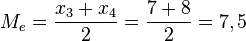 .
.
Datos agrupados
Al tratar con datos agrupados, si 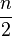 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
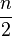 coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:
coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abcisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:Dónde Ni y Ni − 1 son las frecuencias absolutas acomuladas tales que  , ai − 1 y ai son los extremos, inferior y superior, del intervalo donde se alcanza la mediana y Me = ai − 1 es la abscisa a calcular, la moda. Se observa que ai − ai − 1 es la amplitud de los intervalos seleccionados para el diagrama.
, ai − 1 y ai son los extremos, inferior y superior, del intervalo donde se alcanza la mediana y Me = ai − 1 es la abscisa a calcular, la moda. Se observa que ai − ai − 1 es la amplitud de los intervalos seleccionados para el diagrama.
 , ai − 1 y ai son los extremos, inferior y superior, del intervalo donde se alcanza la mediana y Me = ai − 1 es la abscisa a calcular, la moda. Se observa que ai − ai − 1 es la amplitud de los intervalos seleccionados para el diagrama.
, ai − 1 y ai son los extremos, inferior y superior, del intervalo donde se alcanza la mediana y Me = ai − 1 es la abscisa a calcular, la moda. Se observa que ai − ai − 1 es la amplitud de los intervalos seleccionados para el diagrama.Ejemplos para Datos sin agrupar
Ejemplo 1: Cantidad (N) impar de datos
xi fi Ni 1 2 2 2 2 4 3 4 8 4 5 13 5 8 21 > 19.5 6 9 30 7 3 33 8 4 37 9 2 39
Las calificaciones en la asignatura de Matemáticas de 39 alumnos de una clase viene dada por la siguiente tabla:
Calificaciones 1 2 3 4 5 6 7 8 9 Número de alumnos 2 2 4 5 8 9 3 4 2
Primero se hallan las frecuencias absolutas acumuladas Ni. Así, aplicando la formula asociada a la mediana para n impar, se obtiene X(39 + 1) / 2 = X20.- Ni-1< n/2 < Ni = N19 < 19.5 < N20
Por tanto la mediana será el valor de la variable que ocupe el vigésimo lugar.En este ejemplo, 21 (frecuencia absoluta acumulada para Xi = 5) > 19.5 con lo que Me = 5 puntos, la mitad de la clase ha obtenido un 5 o menos, y la otra mitad un 5 o más.[editar]Ejemplo 2 : Cantidad (N) par de datos
Las calificaciones en la asignatura de Matemáticas de 38 alumnos de una clase viene dada por la siguiente tabla (debajo):
Calificaciones 1 2 3 4 5 6 7 8 9 Número de alumnos 2 2 4 5 6 9 4 4 2
xi fi Ni+w 1 2 2 2 2 4 3 4 8 4 5 13 5 6 19 = 19 6 9 28 7 4 32 8 4 36 9 2 38
Primero se hallan las frecuencias absolutas acumuladas Ni. Ni. Así, aplicando la fórmula asociada a la mediana para n par, se obtiene X(38 / 2) = X19.- Ni-1< n/2 < Ni = N18 < 19 < N19
Con lo cual la mediana será la media aritmética de los valores de la variable que ocupen el decimonoveno y el vigésimo lugar. En el ejemplo el lugar decimonoveno lo ocupa el 5 y el vigésimo el 6 con lo que Me = (5+6)/2 = 5,5 puntos, la mitad de la clase ha obtenido un 5,5 o menos y la otra mitad un 5,5 o más.
Moda EstadísticaHablaremos de una distribución bimodal de los datos cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:  Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal.
Siendo la frecuencia absoluta del intervalo modal las frecuencias absolutas de los intervalos anterior y posterior, respectivamente, al intervalo modal. 
Moda en datos agrupadosPara obtener la moda en datos agrupados se usa la siguiente fórmula:
Donde:Li − 1 = Límite inferior de la clase modal.
D1 = Frecuencia absoluta modal sobre la clase contigua inferior.
D2 = Frecuencia absoluta modal sobre la clase contigua superior.
i = intervalo.
Ejemplo
Encontrar la estatura modal de un grupo que se encuentra distribuido de la siguiente forma:
Entre 1.70 y 1.80 hay 8 estudiantes.
Entre 1.60 y 1.70 hay 10 estudiantes.
Entre 1.50 y 1.60 hay 4 estudiantes.

D1 = Frecuencia absoluta modal sobre la clase contigua inferior.
D2 = Frecuencia absoluta modal sobre la clase contigua superior.
i = intervalo.
Ejemplo
Entre 1.70 y 1.80 hay 8 estudiantes.
Entre 1.60 y 1.70 hay 10 estudiantes.
Entre 1.50 y 1.60 hay 4 estudiantes.
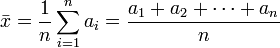
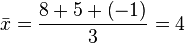
No hay comentarios:
Publicar un comentario